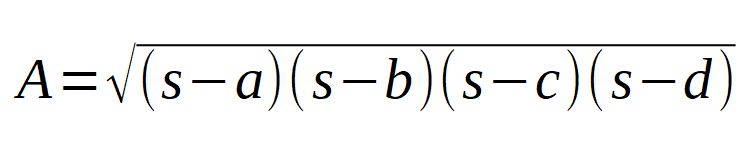zurück Home	Vieleck
allgemeines	Geometrie der Ebene	Vielecke sind Flächen mit n gradlinigen Begrenzungen
Dreieck
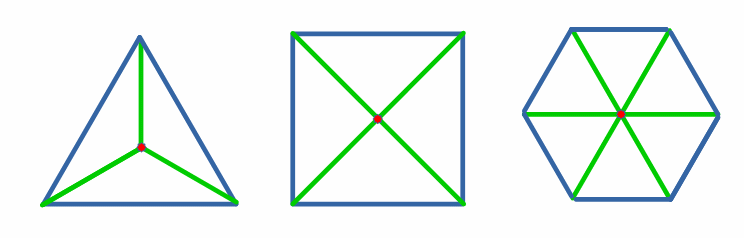
regelmäßiges, gleichseitiges Vieleck	Gleichseitige Vielecke mit n gleichen Seiten (blau) lassen sich in n gleichschenklige Dreiecke (grün) mit dem Mittelpunkt M (rot) zerlegen.
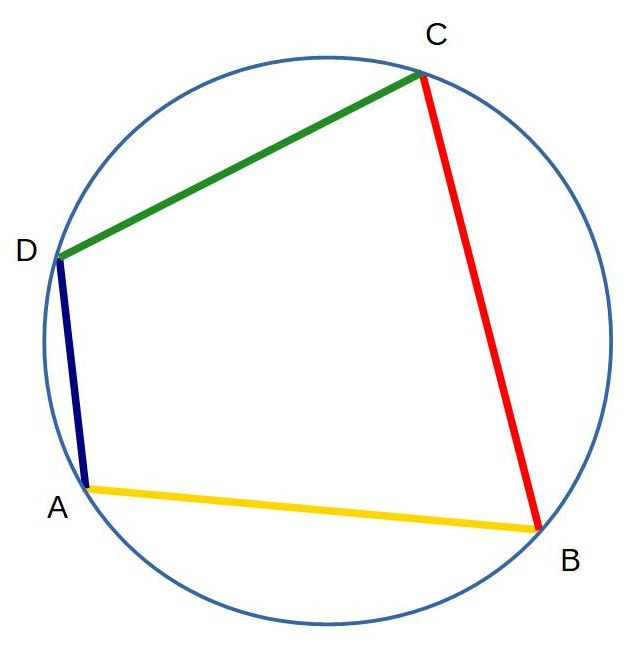
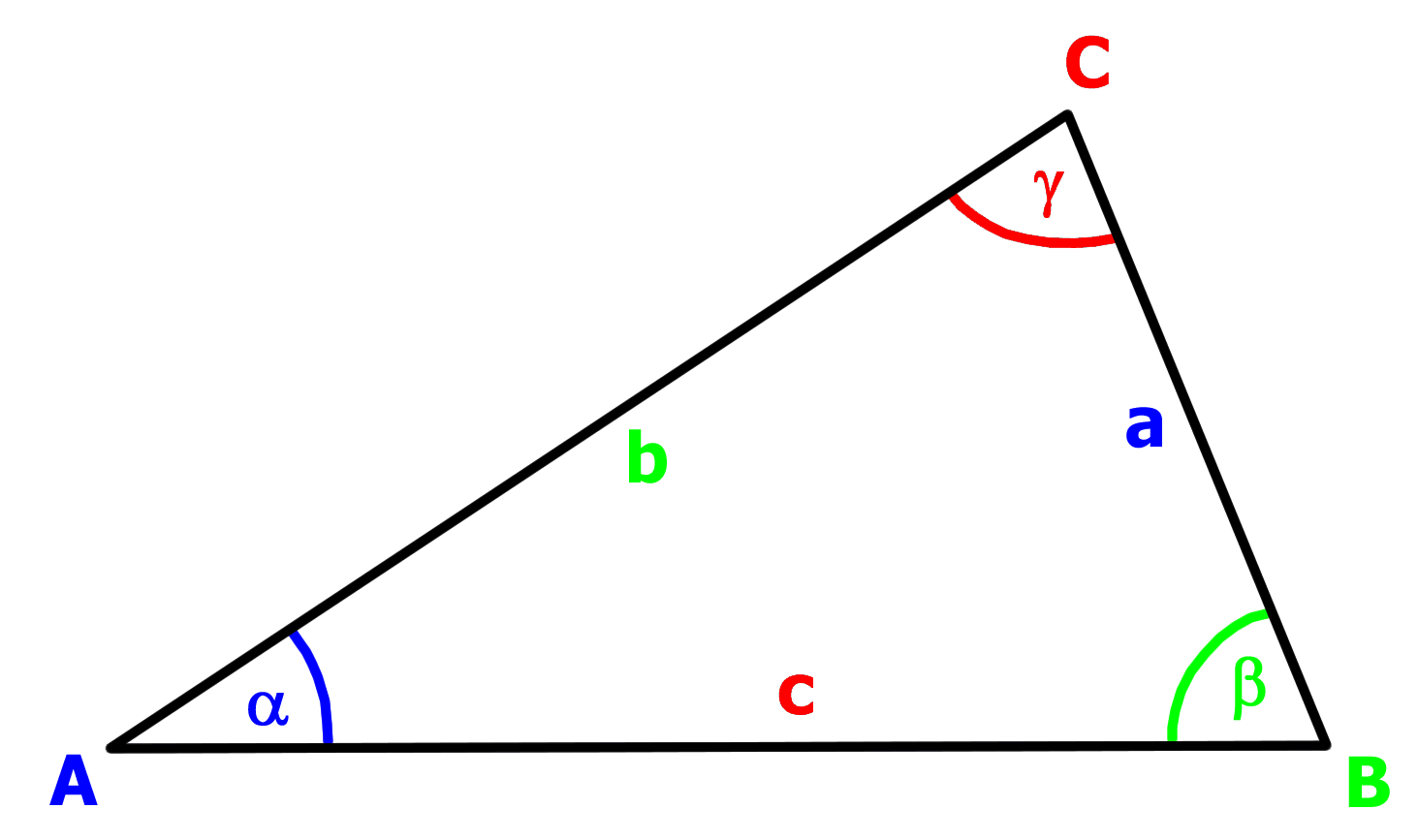
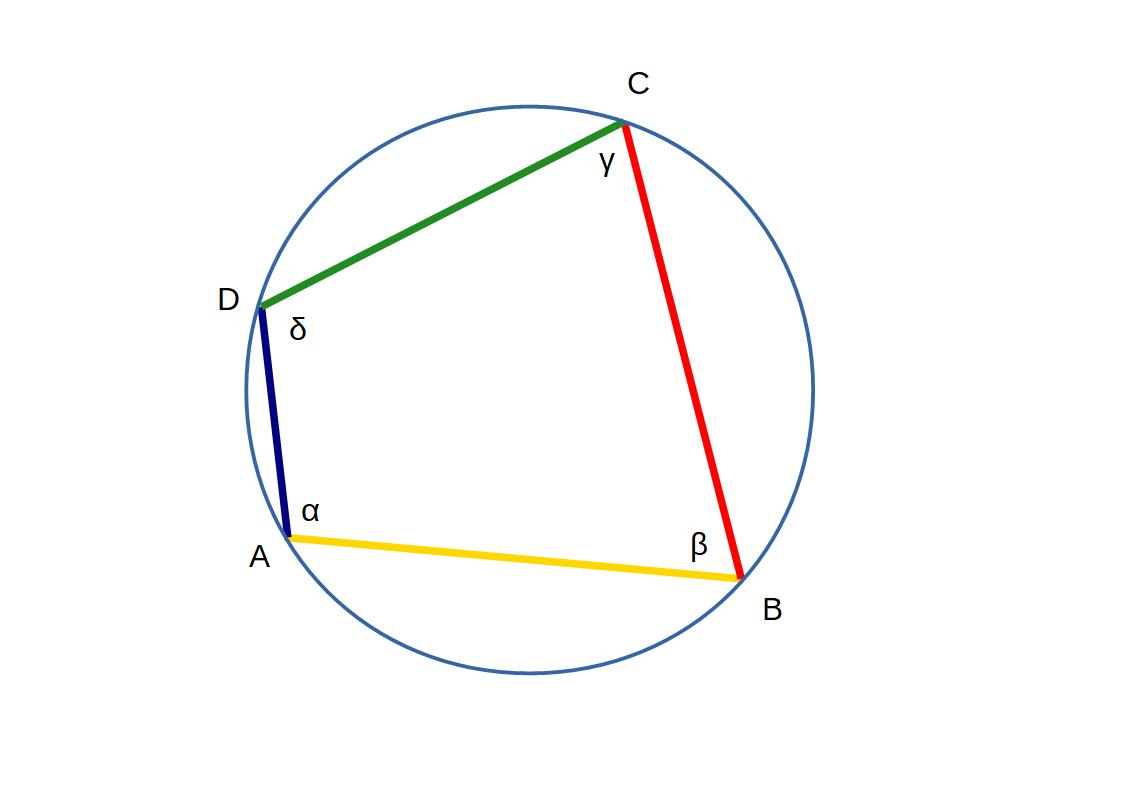
Sehnen - Viereck	Sehnen - Viereck: A, B, C, D	Sehnen - Viereck: Winkel α, β, γ, δ α + γ = 180° β + δ = 180°
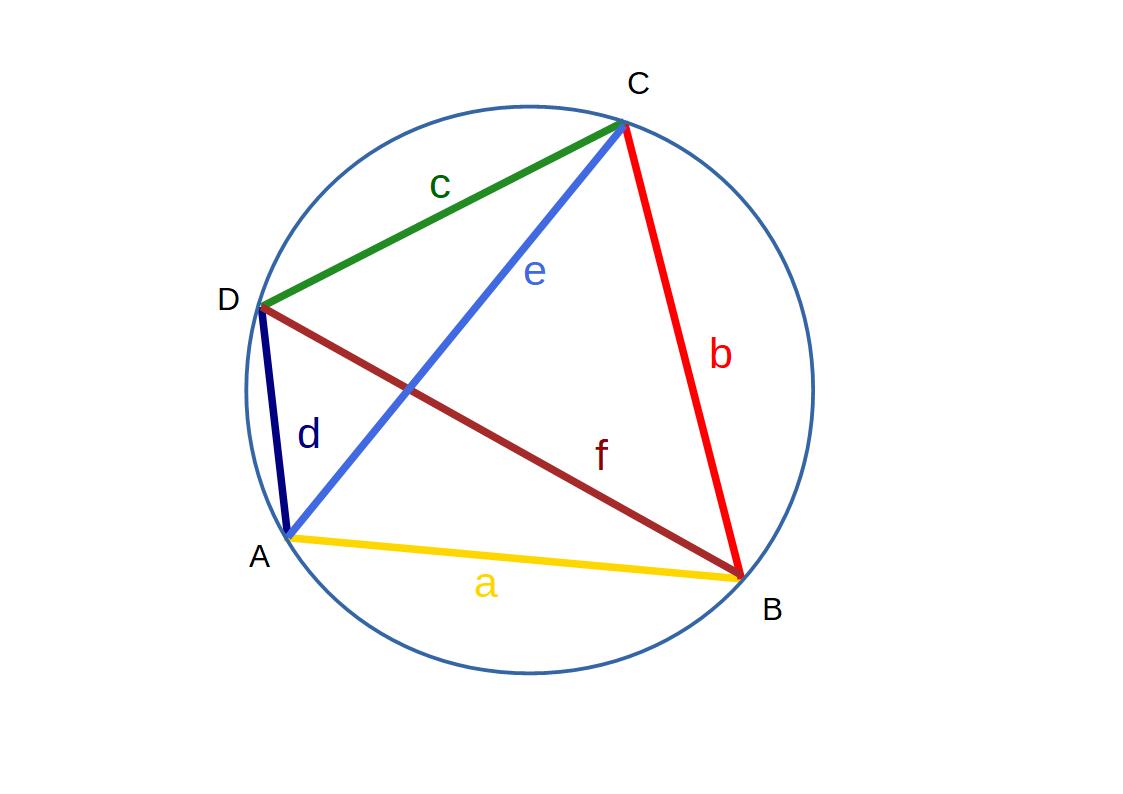
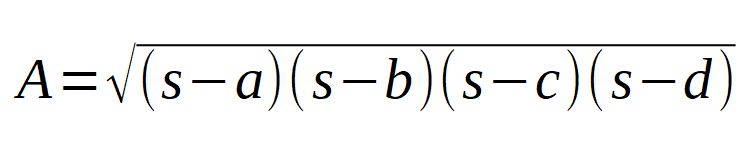
	Sehnen - Viereck: Seite a, b, c, d Diagonalen e, f a * c + b * d = e * f Satz des Ptolemäus	Fläche des Sehnenvierecks: mit S = (a + b+c+d)/2
Tangenten - Viereck	Tangenten - Viereck mit den Eckpunkten A,B,C.D und den Seiten a,b,c und d.	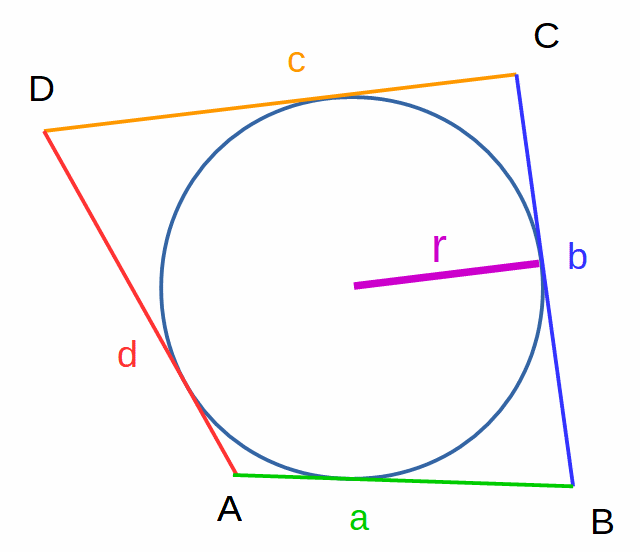A = r * s mit s = (a + b + c + d) / 2 = U / 2 A: Fläche des Tangenten - Vierecks
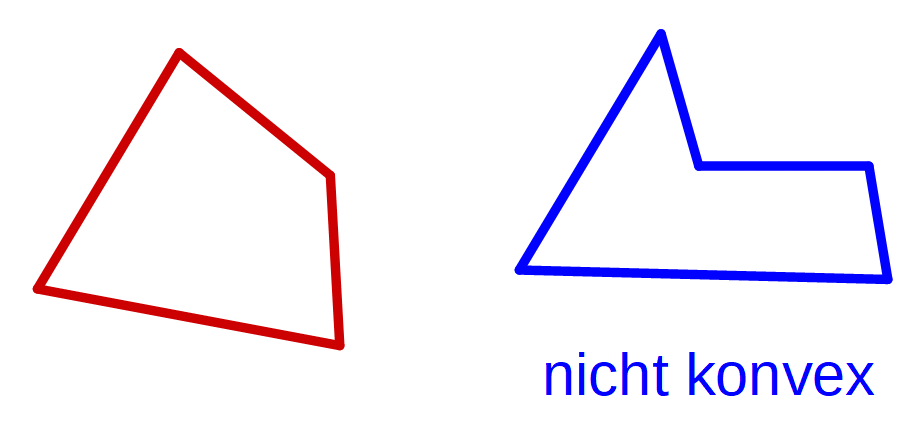
konvexes Vieleck	Aus 5 willkürlich auf einer Ebene verteilten Punkten, von denen keine 3 auf einer Geraden liegen, kann immer ein konvexes Viereck konstruiert werden.		Vermutung von Erdös und Szekeres:  Unter (2n–2 + 1) Punkten findet man immer ein konvexes n-Eck.

Impressum                         Zuletzt geändert am 27.03.2017 16:45