M = {blau, gelb, rot}
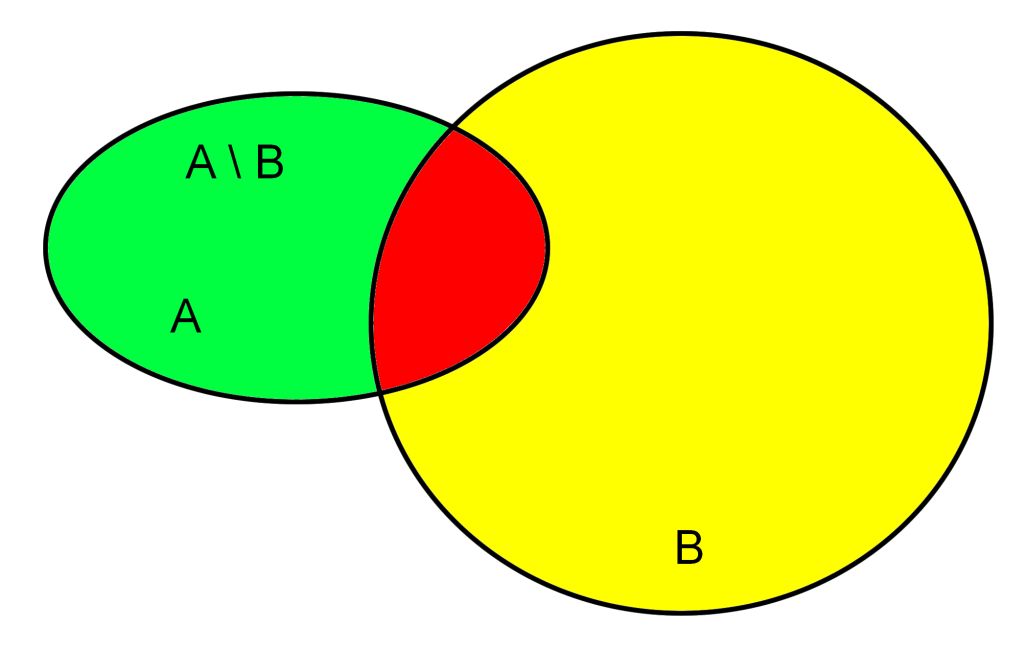
A \ B: nur grün ohne rot, A ohne B
B = {x,y,z}
B X A = { (x;1),(x;2),(y;1),(y;2),(z;1),(z;2)}
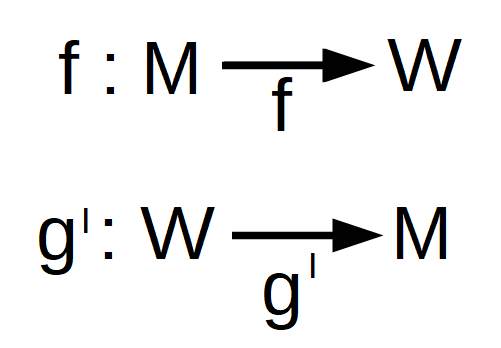

| zurück Home | Mengenlehre | |||
| allgemeines | ||||
| Menge | Eine Menge besteht aus Elementen. | Die Elemente haben keine Reihenfolge. | ||
| leere Menge | Enthält keine Elemente | |||
| Elemente | x ∈ M | x ist ein Element der Menge M | ||
| Beispiele | aufzählende Form: M = {blau, gelb, rot} |
Menge der geraden Zahlen: G = { 4, 6, 8, 10, … } | M10 = {X | X ist eine Ziffer im Dezimalsysten} | |
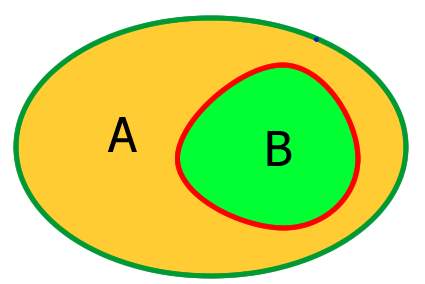
| Teilmenge | B ⊆ A | B ist eine Teilmenge von A  |
||
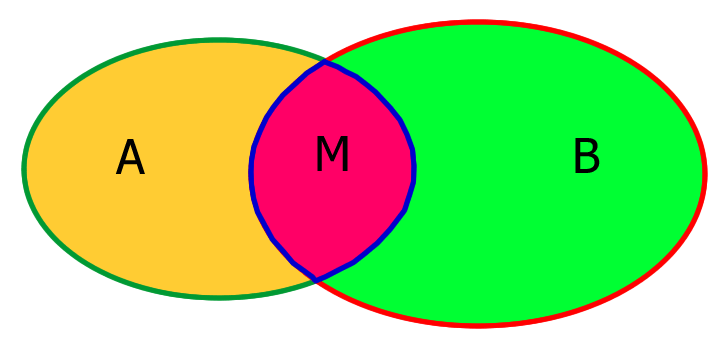
| Schnittmenge | M = A ∩B | M gleich A und B  |
||
| Differenz, Restmenge | D = A \ B | A: grün + rot, B: gelb + rot A \ B: nur grün ohne rot, A ohne B  |
||
| Kartesisches Produkt, Kreuzprodukt | A ( {1,2} B = {x,y,z} |
A X B = { (1;x),(1;y),(1;z),(2;x),(2;y),(2;z)}
B X A = { (x;1),(x;2),(y;1),(y;2),(z;1),(z;2)} |
A X B ≠ B X A | |
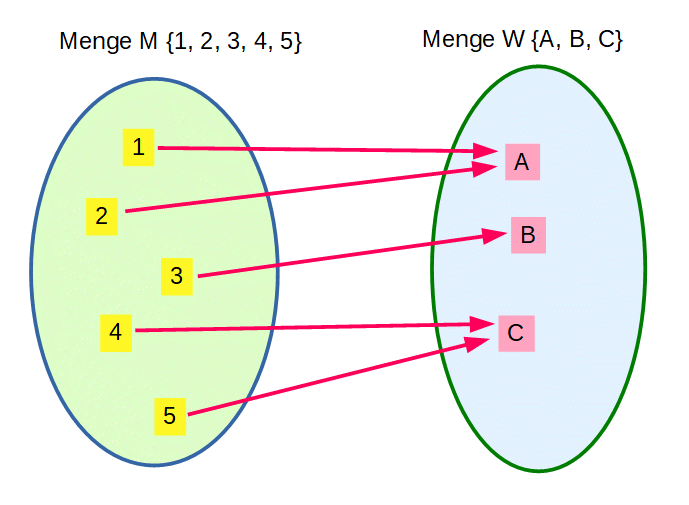
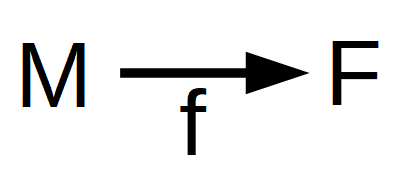
| Abbildung |  |
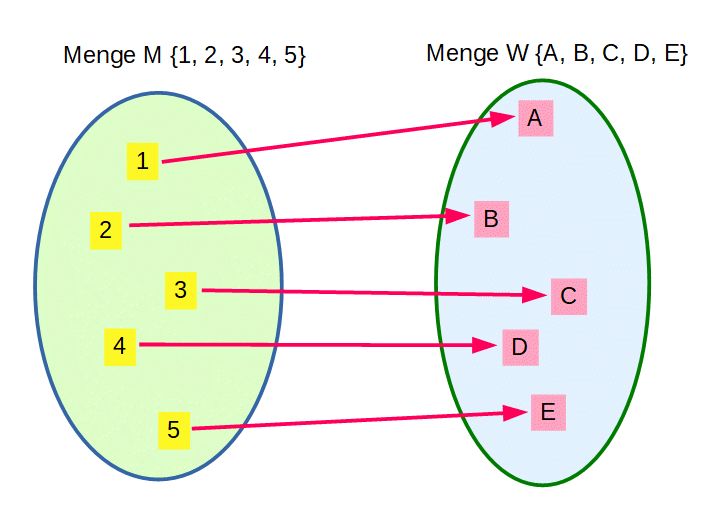
Eine Abbildung f ordnet jedem Element von M Element von W zu. |
||
| umkehrbar eindeutige Abbildung |
 |
Die Elemente von M und W sind einander eindeutig zugeordnet. Bijektion,
bijektive Abbildung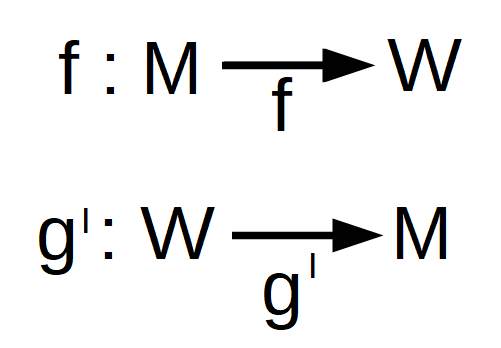 | ||
| geordnete Menge | Aus a < b und b < c folgt a < c | Bespiel rationale Zahlen 1,2,3,4 ... | ||
| Ramsey-Theorie | Jede große ungeordnete Menge - insbesondere willkürlich verteilte Punkte auf einer Ebene - enthält stets eine geordnete Teilmenge. | |||
 |
||||
Impressum Zuletzt geändert am 10.09.2014 17:14